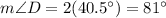Question

Find x, where a=14 degrees and b=22 degrees. Find the measure of each angle of the polygon. Shown below.

Answer 1

To answer this question, we need to remember that the sum of the interior angles of a quadrilateral is equal to 360º (in fact, we can divide a quadrilateral into two triangles, and the sum of interior angles of a triangle is equal to 180º).

Then, we have that a = 14º and b = 22º, then we can state the next equation:

`(2x+14^(\circ))+(3x+22^(\circ))+2x+x=360^(\circ)`

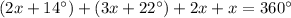
And now, we can solve the equation for x as follows:

1. Add the like terms as follows:

`(2x+3x+2x+x)+14^(\circ)+22^(\circ)=360^(\circ)`
`8x+36^(\circ)=360^(\circ)`

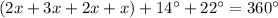
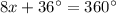
2. Subtract 36º from both sides of the equation:

`8x+36^(\circ)-36^(\circ)=360^(\circ)-36^(\circ)\Rightarrow8x=324^(\circ)`

3. Divide both sides by 8 as follows:

`(8x)/(8)=(324^(\circ))/(8)\Rightarrow x=40.5^(\circ)`

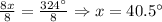
Therefore, the value for x = 40.5º

Then, we can find the values for the measure of angle A as follows:

`m\angle A=2(40.5^(\circ))+14^(\circ)=95^(\circ)`

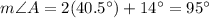
The measure of angle B is

`m\angle B=3(40.5^(\circ)_{})+22^(\circ)=143.5^(\circ)`

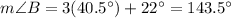
The measure of angle C is

`m\angle C=x^(\circ)=40.5^(\circ)`

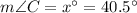
The measure of angle D is

`m\angle D=2(40.5^(\circ))=81^(\circ)`