Question

The length of a rectangular fish pond is 5 feet more than its width. The area of the fish pond is 143 squarefeet. Find the dimensions of the fish pond and its perimeter.What is the length of the fish pond? (Select]What is the width of the fish pond? Select]What is the perimeter of the fish pond? (Select]

Answer 1

We know that the length of the rectangle is 5 feet more than the width. Let x be the width of the rectangle, then its length is x+5. This can be see in the next picture

We also know that the area of the fish pond is 143 and that the area is given by

`A=wl`

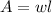
Plugging the values we have that

`143=x(x+5)`

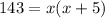
writting the equation in standard form we have that

`\begin{gathered} 143=x(x+5) \\ 143=x^2+5x \\ x^2+5x-143=0 \end{gathered}`

We know that any quadratic equation can be solve by

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

using it for our equation we have

`\begin{gathered} x=\frac{-5\pm\sqrt[]{(5)^2-4(1)(-143)}}{2(1)} \\ =\frac{-5\pm\sqrt[]{25+572}}{2} \\ =\frac{-5\pm\sqrt[]{597}}{2} \\ \text{then} \\ x_1=\frac{-5+\sqrt[]{597}}{2}=9.72 \\ \text{and} \\ x_2=\frac{-5-\sqrt[]{597}}{2}=-14.72 \end{gathered}`

As we know the quadratic equation leads to two solutions. Nevertheless the negative solution is not right in this case, since the distances have to be positive. Then x=9.72.

Once we have the value of x we can know the width a lenght

`\begin{gathered} l=9.72 \\ w=14.72 \end{gathered}`

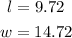
And the perimeter is

`\begin{gathered} P=2w+2l \\ =2(14.72)+2(9.72) \\ =48.88 \end{gathered}`

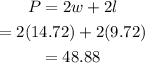
The perimeter is 48.88 ft.