Question

With the following information: Volume of vinegar 25 mL Mass of sodium bicarbonate 1 g Initial temperature of vinegar 17 °C Final temperature of vinegar 14 °C Change in temperature °C (∆T) ?? (answer needed) Calculate the approximate enthalpy of the reaction in joules. Estimate that 1.0 mL of vinegar has the same thermal mass as 1.0 mL of water. Ignore the thermal mass of the sodium bicarbonate. Note: It takes about 4.2 joules (J) to change 1.0 gram (1.0 mL) of water 1.0 °C.

Answer 1

First, let's calculate the change in temperature, which results in making the next subtraction:

`\Delta T=\text{ T}_(fin)\text{ - T}_(in)=\text{ 14\degree C-17\degree C= -3\degree C}`

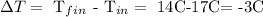
Now, let's calculate the enthalpy of the reaction with the next assumptions:

`\begin{gathered} -\Delta H_r=\text{ Q}_(sen)^(vinegar)+\text{ Q}_(sen)^(NaHCO_3) \\ \\ As\text{ we are told in the exercise, we ignore the second term. Then:} \\ \\ -\Delta H_r=\text{ Q}_(sen)^(vinegar) \end{gathered}`

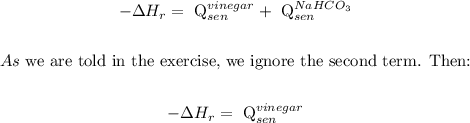
We also have to make the following assumptions: the vinegar's thermal mass and density are the same as the water's. Then, we can make the calculation:

`\begin{gathered} Q_(sen)^(vinegar)=\text{ m*Cp*}\Delta T \\ \\ Where\text{ m is the mass. } \\ Cp\text{ is the specific thermal capacity. } \\ \Delta T\text{ is the change in temperature. } \end{gathered}`
`Q_(sen)^(vinegar)=\text{ 25 mL * }\frac{1\text{ g}}{1\text{ mL}}*\text{ 4.2 }(J)/(g*^oC)*(-3^oC)=\text{ -315 J = -}\Delta H_r`

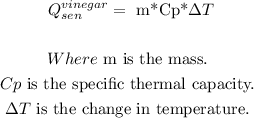
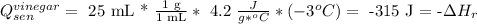
So, the reaction enthalpy equals 315 J approx.