Since the given equation is
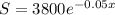
S is the amount of the daily sales from ending to x days
Since the form of the exponential function is
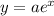
Where a is the initial amount (value y at x = 0)
Then 3800 represents the daily sales when x = 0
Since x = 0 at the ending of the campaign, then
a. The daily sales when the campaign ended is $3800
Since the daily sales will be below half $3800 after x days
Then find half 3800, then equate S by it, then find x
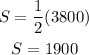
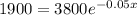
Divide both sides by 3800
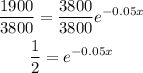
Insert ln for both sides
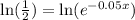
Use the rule
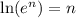
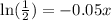
Divide both sides by -0.05 to find x
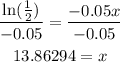
Since we need it below half 3800, then we round the number up to the nearest whole number
Then x = 14 days
b. 14 days will pass after the campaign ended