The graph that shows the transformation of the function f(x) = e^x is option D.
Step - by - Step Explanation
What to find? The transformation of the function f(x)=e^x.
Given:
• f(x) = 4^x
,
• Vertially compresses by a factor 1/3
,
• Translated four units to the right.
,
• Translated down five units.
Note that:
• If f(x) shifts up m- units, then we have f(x) + m.
,
• If f(x) shifts down n-units then we have f(x) - n.
,
• If f(x) shifts right p - units, then we have f(x - p).
,
• If f(x) shifts left q - units, then we have f(x+q).
From the given question, f(x) is translated four units to the right., hence e^x becomes eˣ⁻⁴
f(x) is further compressed by a factor of 1/3, the function becomes 1/3 eˣ⁻⁴.
Finally, the function is translated down five units, hence, the function becomes:
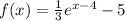
The graph of the function after the translation is