Given the equation of an elipse
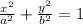
from the question,
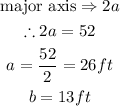
Given that
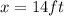
Substitute, for a,b, and x in the elipse formula to find y
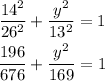
Multiply through by 169
![\begin{gathered} 49+y^2=169 \\ y^2=169-49 \\ y^2=120 \\ y=\sqrt[]{120}=10.95ft \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/jfwmdpqh0mj7mgcc18jl96h9lp5n6q46nc.png)
Hence, it clear the arch because the height of the archway of the bridge 7 feet from the center is approximatelyfeet