Step 1
State the equation of a circle

Where
h= -7
k= 7
Step 2
Find r
r is the distance between the origin and (-7,7)
Distance between 2 points is
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2^{}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/hiqoppg5utntyxsi3z9tdr166xz41i4dz0.png)
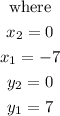
Hence the distance is given as
![\begin{gathered} d=\sqrt[]{(0-(-7))^2+(0-7)^2} \\ d\text{ =}\sqrt[]{49+49} \\ d=\sqrt[]{98} \\ d=7\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/g82yxhkggs3c3ih3y996qcxyzun3dodvo8.png)
Hence r =7√2
Step 3
Write the equation in standard form after substitution.
![\begin{gathered} (x-(-7))^2+(y-7)^2=(7\sqrt[]{2})^2 \\ (x+7)^2+(y-7)^2=(7\sqrt[]{2})^2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/lnr4zbwzwccqevasdpuldx8ih7eqnvopq1.png)