Question

Suppose the main income of firms in the industry for a year is $80 million with a standard deviation of $13 million. If incomes for the industry are distributed normally what is the probability that a randomly selected firm will earn less than $96 million? Round your answer to four decimal places

Answer 1

Given that

The mean income of firms in the industry for a year is $80 million with a standard deviation of $13 million. and we have to find the probability that a randomly selected firm will earn less than $96 million.

Explanation -

We have to find the probability that a firm will earn less than $96 million.

The mean is $80 and the standard deviation is $13.

Then, it is written as

`\begin{gathered} P(x<96)=P(z<(96-80)/(13)) \\ \\ The\text{ formula to find the z is \lparen here z is the z value\rparen} \\ z=(x-\mu)/(\sigma) \\ \mu\text{ is mean and }\sigma\text{ is the standard deviation.} \\ \\ P(<96)=P(z<(16)/(13))=P(z<1.2) \end{gathered}`

The table to find the z value is

According to the z table, the value will be

`\begin{gathered} P(x<96)=P(z<1.2)=0.8849 \\ P(x<96)=88.49\% \end{gathered}`

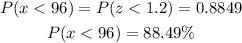
Hence, 88.49% of the randomly selected firms will earn less than $96.

So the probability will be 0.8849.

Final answer -

The final answer is 0.8849 or 88.49%.