Given:
ground to building top is 30 degrees.
Distance = 400 feet
The angle of elevation at is top of the building = 52 degrees.
Find-: Height of the building.
Sol:
For the triangle ABC
Perpendicular = Height
Base = x
Angle = 52
Use trigonometric formula:
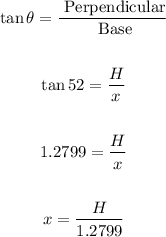
For the triangle ABD is:
Perpendicular = Height
Base = x+400
Angle = 32

Put the value of "x" is:
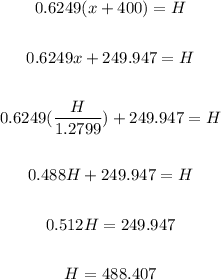
So the height of the building is: 488.407 feet