The formula to calculate Simple Interest is given as
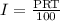
The question provides the following parameters:
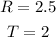
If the amount to be had now is $4000, which is inclusive of the interest to be had over the period, this means that
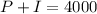
If we substitute the value for I, we have a new equation, such that
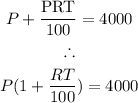
Substituting the values into the equation, we can solve for P as
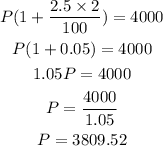
The answer is $3,809.52