Answer:
A) The initial size o the culture is 640
B) The doubling period is 47 minutes
C) The population after 60 minutes is 1563
D) The population will reach 13000 after 3 hours 22 minutes
Step-by-step explanation:
The form of an exponential grow model is:
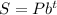
Where:
S is the population after t hours
P is the initial population
b is the base of the exponent
t is the time, in hours
We know that after 15 minutes, the population was 800. 15 minutes is a quarter of an hour. Thus, t = 1/4, S = 800:
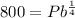
Also, we know that after 30 minutes, the population was 1000. Thus, t = 1/2, S = 1000
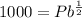
Then, we have a system of equations:
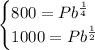
We can solve the first equation for P:
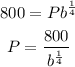
And substitute in the other equation:
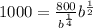
And solve:
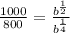
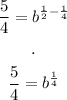
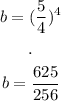
Now, we can find the initial population P:
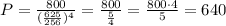
The initial population is 640
To find the doubling period, we want that the population equal to twice the initial population:
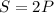
Then, since we know the equation, we can write:
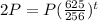
Then:
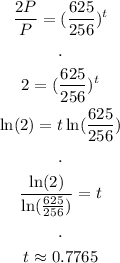
If an hour is 60 minutes:
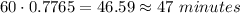
To find the population after 60 minutes, we use t = 1 hour and we want to find S:
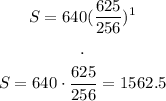
To find when the population is 13000, then we use S = 13000 and solve for t:
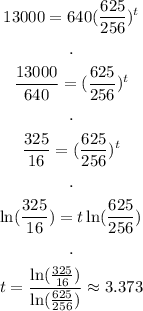
We have 3 full hours and 0.373. Since one hour is 60 minutes:
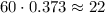
The population reach 13000 after 3 hours 22 minutes