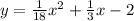Question

Write the equation of the function in vertex form, then convert to standard form.

Answer 1

The equation of the parabola in vertex form is

`y=a(x-h)^2+k`

where the point (h,k) is the coordinate of the vertex. From our picture, we can note that (h,k)=(-6,-4).

By substituting these values into our first equation, we have

`y=a(x-(-6))^2-4`

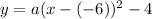
which gives

`y=a(x+6)^2-4`

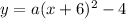
Now, we can find the constant a by substituting one of the other given point. If we choose point (0,-2) into this last equation, we get

`-2=a(0+6)^2-4`

which gives

`\begin{gathered} -2=a(6^2)-4 \\ -2=36a-4 \end{gathered}`

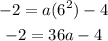
then, by moving -4 to the left hand side, we have

`\begin{gathered} -2+4=36a \\ 2=36a \\ or\text{ equivalently,} \\ 36a=2 \end{gathered}`

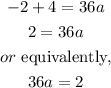
and finally, a is equal to

`\begin{gathered} a=(2)/(36) \\ a=(1)/(18) \end{gathered}`

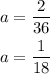
hence, the equation of the parabola in vertex form is

`y=(1)/(18)(x+6)^2-4`

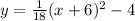
Now, lets convert this equation into a standrd form. This can be done by expanding the quadratic term and collecting similar term. That is, by expanding the quadratic terms, we obtain

`y=(1)/(18)(x^2+12x+36)-4`

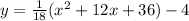
now, by distributing 1/18, we have

`y=(1)/(18)x^2+(12)/(18)x+(36)/(18)-4`

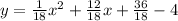
which is equivalent to

`y=(1)/(18)x^2+(1)/(3)x+2-4`

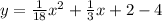
and finally, the parabola equation in standard form is

`y=(1)/(18)x^2+(1)/(3)x-2`