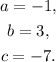Recall that the quadratic formula states that the solution to the quadratic equation:

are:
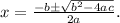
Notice that a is the coefficient of the quadratic part, b is the coefficient of the linear part and c is a constant.
We can rewrite the given equation as follows:
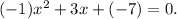
Therefore, the values a, b, and c that should be used in the quadratic formula to compute the solutions to the quadratic equation:
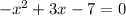
are:
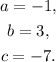
Answer: