We have the following rectangular garden
The perimeter is 202 feet, we can do the following equality
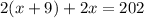
Now we solve "x"
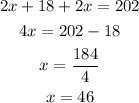
Now, we know the longer (l = 55) and the width (w = 46)
To find the area we use the following equation
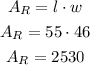
In conclusion, the area of the garden is 2530 square feet