Question

How do you use the distance formula to figure out the area of the triangle. I don't really know how to solve this problem or use distance formula

Answer 1

The Area of a Right Triangle

The area of any triangle of base B and height H is:

`A=(B\cdot H)/(2)`

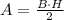
The base and the height must be perpendicular, i.e, the angle between them must be 90°.

The trick here is to prove the triangle is right at the point (15, 5).

If two lines are perpendicular, the product of their slopes is -1.

Calculate the slope of the line that joins the vertices at (5, 15) and (15, 5):

`\begin{gathered} m_1=(5-15)/(15-5) \\ m_1=-(10)/(10) \\ m_1=-1 \end{gathered}`

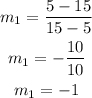
Calculate the slope of the line that joins the vertices at (20, 10) and (15, 5);

`\begin{gathered} m_2=(5-10)/(15-20) \\ m_2=(-5)/(-5) \\ m_2=1 \end{gathered}`

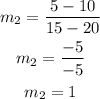
It can be verified that m1 * m2 = -1, thus the lines are perpendicular and we can use the formula given above to compute the area.

Find the length of both lines with the formula of the distance:

`\begin{gathered} L_1=\sqrt[]{(5-15)^2+(15-5)^2} \\ \text{Calculating:} \\ L_1=\sqrt[]{200} \end{gathered}`
`\begin{gathered} L_2=\sqrt[]{(5-10)^2+(15-20)^2} \\ L_2=\sqrt[]{50} \end{gathered}`

Apply the formula of the area:

`\begin{gathered} A=\frac{\sqrt[]{200}\cdot\sqrt[]{50}}{2} \\ A=\frac{\sqrt[]{10000}}{2} \\ A=(100)/(2)=50 \end{gathered}`

The area is 50 square units