Question

Find greatest common factor for each group,factor completely and find real roots

Answer 1

Write out the polynomial given

The first group of the expresion is

`\begin{gathered} 3x^3+4x^2 \\ \text{Then the GCE is } \\ x^2((3x^3)/(x^2)+(4x^2)/(x^2)) \\ \text{GCE}=x^2 \end{gathered}`

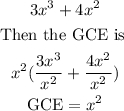
GCE is x²

For the second group, we have

`\begin{gathered} 75x+100 \\ \text{GCE}=25((75x)/(25)+(100)/(25)) \\ \text{GCE}=25 \end{gathered}`

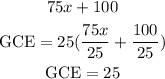
The GCE for the secod group is 25

To factorise completely, we have

`\begin{gathered} 3x^3+4x^2+75x+100 \\ \\ x^2((3x^3)/(x^2)+(4x^2)/(x^2))+25((75x)/(25)+(100)/(25)) \end{gathered}`

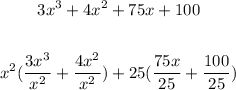
Then by simplification, we have

`\begin{gathered} x^2(3x+4)+25(3x+4) \\ \text{Then, we factor completely to get} \\ (3x+4)(x^2+25) \end{gathered}`

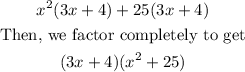
Then factors are (3x +4)(x²+ 25)

To find the real root, we equate each of the factors to zero, hence

`\begin{gathered} (3x+4)(x^2+25)=0 \\ \text{Then} \\ 3x+4=0orx^2+25=0 \\ 3x=-40rx^2=-25 \\ \end{gathered}`

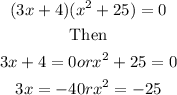
Thus

`\begin{gathered} (3x)/(3)=-(4)/(3) \\ x=-(4)/(3)\text{ is a real root } \\ or\text{ } \\ x^2=-25 \\ \text{take square root} \\ x=\pm_{}\sqrt[]{-25}\text{ not a real root} \end{gathered}`

Therefore, since the root of -25 is a complex number,

The only real root is x = -4/3