Let,
x₁, y₁ = 2, 2
x₂, y₂ = 6, 10
a.) The slope of the line.
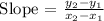
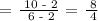
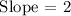
Therefore, the slope of the line is 2.
b.) The y-intercept of the line.
Substitute slope = m = 2 and x, y = 2, 2 in y = mx + b
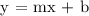

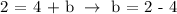
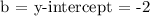
Therefore, the y-intercept is -2.
For us to answer the other 2 questions, let's first complete the equation of the graph.
Substitute slope = 2 and y-intercept = -2 in the y = mx + b
y = mx + b
y = (2)x + (-2)
y = 2x - 2
The equation of the line is y = 2x - 2
c.) Finding the value of a.
x = a
y = 8
We get,
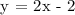
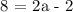
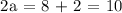
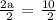
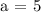
Therefore a = 5
d.) Finding the value of b.
x = 4
y = b
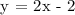
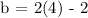
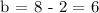
Therefore, b = 6