Question

Determine the number of solutions for the following system of linear equations. If there is only onesolution, find the solution.x + 3y – 2z = 6- 4x - 7y + 3z = 3- 7x – 4y - 3z = -5AnswerKeypadKeyboard ShortcutsSelecting an option will enable input for any required text boxes. If the selected option does not have anyassociated text boxes, then no further input is required.O No SolutionO Only One SolutionX =y =Z=Infinitely Many Solutions

Answer 1

First, let's clear z from equation 1:

`\begin{gathered} x+3y-2z=6\rightarrow x+3y-6=2z \\ \rightarrow z=(1)/(2)x+(3)/(2)y-3 \end{gathered}`

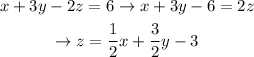
Now, let's plug it in equations 2 and 3, respectively:

`\begin{gathered} -4x-7y+3z=3 \\ \rightarrow-4x-7y+3((1)/(2)x+(3)/(2)y-3)=3 \\ \\ \rightarrow-4x-7y+(3)/(2)x+(9)/(2)y-9=3 \\ \\ \rightarrow-(5)/(2)x-(5)/(2)y=12_{} \\ \end{gathered}`
`\begin{gathered} -7x-4y-3z=-5 \\ \rightarrow-7x-4y-3((1)/(2)x+(3)/(2)y-3)=-5 \\ \\ \rightarrow-7x-4y-(3)/(2)x-(9)/(2)y+3=-5 \\ \\ \rightarrow-(17)/(2)x-(17)/(2)y=-8 \end{gathered}`

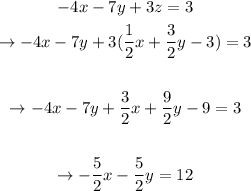
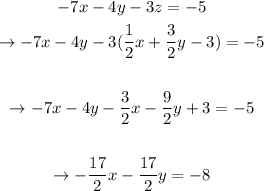
We'll have a new system of equations:

`\begin{gathered} -(5)/(2)x-(5)/(2)y=12_{} \\ \\ -(17)/(2)x-(17)/(2)y=-8 \end{gathered}`

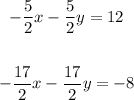
Now, let's simplify each equation. To do so, we'll multiply the first one by -2/5 and the second one by -2/17. We'll get:

`\begin{gathered} x+y=-(24)/(5) \\ \\ x+y=(16)/(17) \end{gathered}`

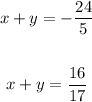
Now, let's solve each equation for y to see them as a pair of line equations:

`\begin{gathered} y=-x-(24)/(5)_{} \\ \\ y=-x+(16)/(17) \end{gathered}`

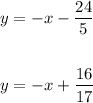
Notice that this lines have the same slope. Therefore, they're parallel and do not intercept.

This way, we can conlcude that the original system has no solution.