The given slope is:
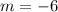
And the point:
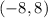
we label the coordinates as follows:
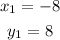
And now, we use the slope-point formula, which is:

substituting the known values of slope m and the point:
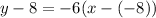
We need to solve this for y to find the slope intercept form (which is y=mx+b):
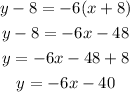
The slope-intercept form is:
y = -6x - 40