Question

#1 An airplane rises at an angle of 14° with the ground. Find, to the nearest 10 feet, the distance it has flown when it has covered a horizontal distance of 1500 feet.

Answer 1

The airplane rises at an angle of 14° with respect to the ground.

You have to find the distances (diagonal) that it frew if it covered a horizontal distance of 1500 feet.

The distance flew by the place with respect to the horizontal ground and the height the plane is at after traveling 1500 feet form a right triangle. Where x represents the hypothenuse of the triangle. To determine its measure, you have to use the trigonometric relations

`\begin{gathered} \sin \theta=(opposite)/(hypohtenuse) \\ \cos \theta=(adjacent)/(hypothenuse) \\ \tan \theta=(opposite)/(adjacent) \end{gathered}`

Given that θ=14° and we know that the adjacent side to the angle measures 1500 feet, using the cosine we can determine the length of x as:

`\begin{gathered} \cos 14=(1500)/(x) \\ x\cos 14=1500 \\ x=(1500)/(\cos 14) \\ x=1545.92ft \end{gathered}`

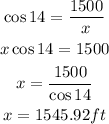
The distance flew by the airplane is 1545.92ft