a)
Since we have a constant angular acceleration we have that:
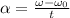
Plugging the values we know we have that:
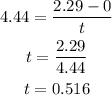
Therefore it will take 0.516 (rounded to three decimals) seconds to achive this angular velocity.
b)
To find how many revolutions he needs we first calculate the change in angular position using the formula:
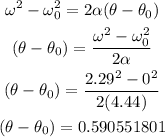
Now we divide this change in angular position by 2pi (the angle equivalent to a revolution) to get the revolutions:
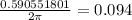
Therefore it takes 0.094 (round to three decimals) revolutions to get to this angular velocity.
c)
The torque is the force by the radius, then we have:
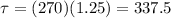
But the torque is also equal to the moment of inertia multiplied by the angular acceleration:
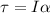
Then we have:
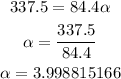
Now we use the formula for angular acceleration to get the time:

Therefore it takes 0.573 seconds to stop the merry go round.