Given:
The initial height of the rock was,
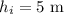
The final height of the rock is,
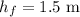
The mass of the rock is,
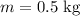
The travelling speed of the rock is,
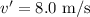
To find:
a) The speed of the rock at Joe's head
b) how much work was done by air resistance
Step-by-step explanation:
The displacement of the rock is,
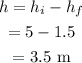
The final speed at Joe's head is,
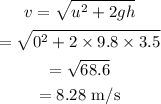
Hence, the speed of the rock at Joe's head is 8.28 m/s.
b)
The speed at Joe's head was 8.0 m/s, and the loss of kinetic energy is,
![\begin{gathered} (1)/(2)* m[(8.23)^2-(8.0)^2] \\ =(1)/(2)*0.5*[3.73] \\ =0.93\text{ J} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/sb976amd8c5yimrj8t5eruyr70fcl2kcuv.png)
This loss of energy is the work done by the air resistance.
Hence, the work done by the air resistance is 0.93 J.