Question

Given sinx= 5/13 andπ/2 < x < π find the exact value of tan 2x

Answer 1

Given sin(x)=5/13

First, lets find cos(x).

It is known that:

`\begin{gathered} \sin ^2(x)+\cos ^2(x)=1 \\ ((5)/(13))^2+\cos ^2(x)=1 \\ \cos ^2(x)=1-(25)/(169) \\ \cos ^2(x)=(169-25)/(169)=(144)/(169) \\ \cos (x)=\pm\sqrt[]{(144)/(169)}\text{ = }\frac{\sqrt[]{144}}{\sqrt[]{169}} \\ \cos (x)=\pm(12)/(13) \end{gathered}`

Since π/2 < x < π, we are in 2nd quadrant. Then, cos(x) is negative.

`\cos (x)=-(12)/(13)`

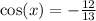
Since we know the values for sin and cos, we can find tan(x):

`\begin{gathered} \tan (x)=(\sin(x))/(\cos(x)) \\ \tan (x)=((5)/(13))/(-(12)/(13)) \\ \tan (x)==-(5)/(12) \end{gathered}`

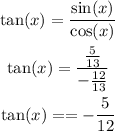
Now, lets work with the expression tan(2x)

It is known that:

`\tan (2x)=(2\tan(x))/(1-\tan^2(x))`

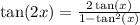
Since we know tan(x), we can substitute in the expression above and find the value of tan(2x):

`\begin{gathered} \tan (2x)=(2\tan(x))/(1-\tan^2(x)) \\ \tan (2x)=\frac{2\cdot(-(5)/(12)_{})}{1-(-(5)/(12))^2} \\ \tan (2x)=(-(10)/(12))/(1-(25)/(144))=(-(10)/(12))/((144-25)/(144))=(-(10)/(12))/((119)/(144))=-(10)/(12)\cdot(144)/(119) \\ \tan (2x)=-(120)/(119) \end{gathered}`

Answer: -120/119