Question

the sum of two numbers is 70 and their difference is 30 ,Find the two numbers using the process of substitution let x=the first number and y=the second number.

Answer 1

Let the first number be x and the second number be y.

Since the sum of the numbers is 70, it follows that the equation that shows the sum of the numbers is:

`x+y=70`

The difference between the two numbers is 30, hence, the equation that shows the difference is:

`x-y=30`

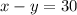
The system of equations is:

`\begin{cases}x+y={70} \\ x-y={30}\end{cases}`

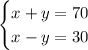
Make x the subject of the first equation:

`x=70-y`

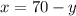
Substitute this into the second equation:

`\begin{gathered} 70-y-y=30 \\ \Rightarrow70-2y=30 \\ \Rightarrow-2y=30-70 \\ \Rightarrow-2y=-40 \\ \Rightarrow(-2y)/(-2)=(-40)/(-2) \\ \Rightarrow y=20 \end{gathered}`

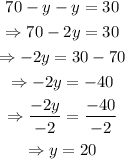
The second number is 20.

Substitute y=20 into the equation x=70-y to find x:

`x=70-20=50`

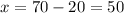
Answers:

The equation that shows the sum of the numbers is x+y=70.

The equation that shows the difference between the numbers is x-y=30.

The numbers are x=50 and y=20.