Question

1.Given the Graph Circle One: Arithmetic, Geometric, or Neither Circle One: Common Ratio or Common difference: recursive formula-explicit formula-find the 5th term-

Answer 1

We can see in the graph that for every increment in x, the y-value is halved (that is, multiplied by 1/2).

Since the y-values are being multiplied for every increment of x, we have a geometric sequence or function.

Also, the function has a common ratio, which is the value 1/2 that multiplies y for every increment of x.

Last, we have a recursive formula: each value of y is half of the previous value of y (a_n = (1/2) * a_(n-1))

In order to find the explicit formula, since we have an exponential function, we can use the model y = a*b^x.

Using the points (1, 32) and (2, 16), we have:

`\begin{gathered} 32=a\cdot b^1\to a=(32)/(b) \\ 16=a\cdot b^2\to b^2=(16)/(a)=(16b)/(32)\to b=(1)/(2) \\ 32=a\cdot(1)/(2)\to a=64 \end{gathered}`

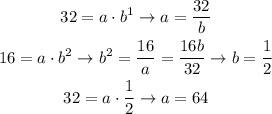
So the explicit function is y = 64 * (1/2)^x.

Looking at the graph, the 5th term of the sequence (x = 5) is found by halving the value y = 8 two times, so the 5th term is 2.