Question

Use a net to find the surface area of the prism.25 cm3.5 cm13 cmThe surface area of the prism is (Simplify your answer.)

Answer 1

A rectangle prism of sides 25, 3.5 and 13 cm can be drawn as:

It will have 6 faces (4 lateral, a base and a top face)

Each face has a surface area that is the product of two of the sides. We have two faces for each pair of sides.

So if we have sides a, b and c, the surface area can be written as:

`S=2(a\cdot b+a\cdot c+b\cdot c)`

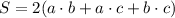
With the sides of our prism we can calculate the surface area as:

Answer: The surface area of the prism is 916 cm^2