Since QP and QB are equal the triangle PQB the angles:
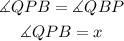
The last angle can be found by adding all the internal angles and making it equal to 180 degrees.
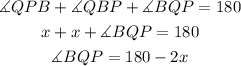
The angle BQP and the angle AQP are suplementary, this means that their sum is equal to 180 degrees. So we have:
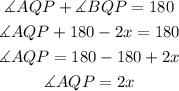
Since the sides AP and PQ are equal, then the angle PAQ is equal to AQP.
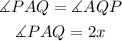
To find the last angle on that triangle we can add all the internal angles and make it to 180 degrees.
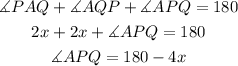
The angle APC is suplementary with the sum of the angles APQ and BPQ. So we have:
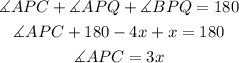
The sides AP and AC are equal, therefore the angles APC and ACP are also equal.
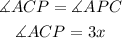
Then we can find the last angle on that triangle.
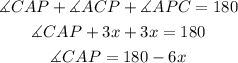
The angle CAB is equal to the sum of CAP and PAQ. So we have:
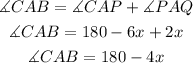
Since the sides AB and BC are equal, then the angles ACB and CAB must also be equal. We can find the value of x with this.
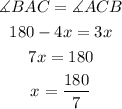
The value of x is 180/7