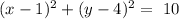Answer:
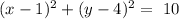
Step-by-step explanation:
The equation of a circle whose center is (a, b) and which has a radius r is given as:
(x - a)² + (y - b)² = r²
For the circle with endpoints at A(-2,3) and B(4,5).
The center (a, b) of the circle is calculated as:
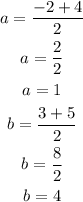
The center, (a, b) = (1, 4)
The diameter(D) of the circle is the distance between the endpoints A(-2,3) and B(4,5).
![\begin{gathered} D=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ D=\sqrt[]{(4-(-2))^2+(5-3)^2} \\ D=\sqrt[]{(4+2)^2+2^2} \\ D=\sqrt[]{6^2+2^2} \\ D=\sqrt[]{36+4} \\ D=\sqrt[]{40} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/rlpdl50gcfh0hk05y65hgmxcooqtbrbz1x.png)
The diameter of the circle = √40
Radius = Diameter / 2
r = d/2
r = √40 / 2
Substituting a = 1, b = 4, and r = √40 / 2 into the general equation of a circle:
![\begin{gathered} (x-1)^2+(y-4)^2=(\frac{\sqrt[]{40}}{2})^2 \\ (x-1)^2+(y-4)^2=(40)/(4) \\ (x-1)^2+(y-4)^2=\text{ 10} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7yifrxcuwm8wl5uszfnws0tln6nm0q39av.png)
The general equation of the circle is: