ANSWER
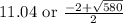
Step-by-step explanation
Given that:
In the figure provided, the triangle EFG is similar to the triangle is ECD
FE = 12
CD = 12
FG = CF + 2
To find the length CF, apply the similarity triangle theorem
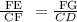
Substitute the given data into the above equation
