Part a.
From the given infomation, the mean is equal to
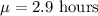
and the standard deviation
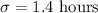
Then, the distribution of X is:
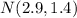
Part b.
In this case, we need to find the following probability:
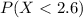
So, in order to find this value, we need to convert the 2.6 hours into a z-value score by means of the z-score formula:
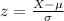
Then, by substituting the given values into the formula, we get
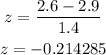
Then, the probability we must find in the z-table is:
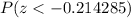
which gives
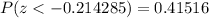
Therefore, by rounding to 4 decimal places, the answer for part b is: 0.4152
Part c.
In this case, we need to find the following probability
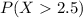
Then, by converting 2.5 to a z-value, we have
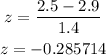
So, we need to find on the z-table:
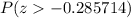
which gives
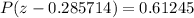
Then, by multiplying this probability by 100% and rounding to the nearest hundreadth,
the answer for part c is: 61.25 %
Part d.
In this case, we have the following information:
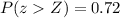
and we need to find Z. From the z-table, we get
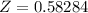
Then, from the z-value formula, we have
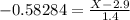
and we need to isolate the amount of hours given by X. Then, by multiplying both sides by 1.4, we obtain
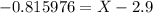
Then, X is given by
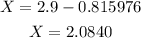
So, by rounding to 4 decimal places, the answer is: 2.0840 hours.