ANSWER
(5, -2) and (0, -3)
Step-by-step explanation
We want to find which of the ordered pairs is a solution to the system of inequalities.
Ordered pairs are written in the form (x, y), this means, whichever ordered pair is a solution, when inserted into the system of inequalities, should be true.
This means that the values of x and y must be true for both inequalities in the system.
The system of inequalities is:
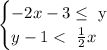
A. (5, -2)

Since both inequalities are correct, this is a solution.
B. (-3, -4)
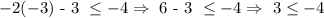
Since the first inequality is already incorrect, we do not need to go further.
It is not a solution
C. (0, -3)
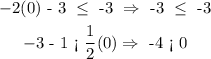
Since both inequalities are correct, this is a solution.
D. (0, 1)
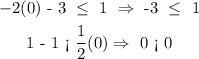
Since 0 is not less than 0, this is not a solution.
E. (-4, 1)
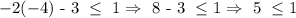
Since 5 is not less than 1, this is not a solution.
Therefore, the solutions are (5, -2) and (0, -3)