Question

A tungsten wire is 1.5m long and has a diameter of A current of flows through the wire. The resistivity of the wire is 5.6 * 10 ^ - 8 What is the potential difference across the ends of the wire?

Answer 1

Complete Question:

A tungsten wire is 1.5 m long and has a diameter of 1.0 mm. A current of 60 mA flows through the wire. The resistivity of the wire is 5.6 * 10^-8 Ωm. What is the potential difference across the ends of the wire?

Answer:

Potential difference, V = 0.00642 Volts.

Step-by-step explanation:

Given the following data;

Diameter = 1 mm to meters = 1/1000 = 0.001 m

Length = 1.5m

Current = 60mA = 60/1000 = 0.06 Amperes.

Resistivity = 5.6 * 10^-8 Ωm

To find the potential difference across the ends of the wire;

First of all, we would determine the cross-sectional area of the wire (circle);

`Radius, r = \frac {diameter}{2}`

`Radius = \frac {0.001}{2}`

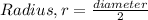
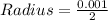
Radius = 0.0005 m

Area of wire (circle) = πr²

Substituting into the above formula, we have;

Area = 3.142 × (0.0005)²

Area = 3.142 × 2.5 × 10^-7

Area = 7.855 × 10^-7 m²

Next, we find the resistance of wire;

Mathematically, resistance is given by the formula;

`Resistance = P \frac {L}{A}`

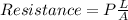
Where;

P is the resistivity of the material.

L is the length of the material.

A is the cross-sectional area of the material.

Substituting into the formula, we have;

`Resistance = 5.6 * 10^(-8) \frac {1.5}{7.855 * 10^(-7)}`

`Resistance = 5.6 * 10^(-8) * 1909611.712`

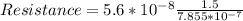
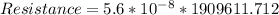
Resistance = 0.107 Ohms.

Now, we can find the potential difference using the formula;

`V = IR`

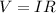
Where;

V represents voltage or potential difference measured in volts.

I represents current measured in amperes.

R represents resistance measured in ohms.

Substituting into the formula, we have;

`V = 0.06*0.107`

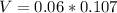
Potential difference, V = 0.00642 Volts.