Question

For the following exercise, find the horizontal intercepts, the vertical intercept, the vertical asymptotes, and the horizontal or slant asymptotes of the function. use that information to sketch graph.

Answer 1

The expression is given below as

`a(x)=(x^2+2x-3)/(x^2-1)`

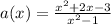
The horizontal intercepts will be at y=0

`\begin{gathered} a(x)=(x^2+2x-3)/(x^2-1) \\ (x^2+2x-3)/(x^2-1)=0 \\ x^2+2x-3=0 \\ x^2+3x-x-3=0 \\ x(x+3)-1(x+3)=0 \\ (x-1)(x+3)=0 \\ x-1=0,x+3=0 \\ x=1,x=-3 \end{gathered}`
`\begin{gathered} x^2-1=0 \\ x^2=1 \\ x=\pm1 \\ x=1,x=-1 \end{gathered}`

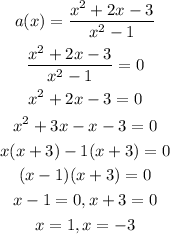
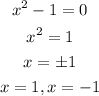
Hence,

The horizontal intercepts is at x = -3

The vertical intercept is at x=0

`\begin{gathered} a(x)=(x^2+2x-3)/(x^2-1) \\ y=(0^2+2(0)-3)/(0^2-1) \\ y=(-3)/(-1) \\ y=3 \end{gathered}`

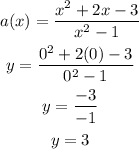
Hence,

The vertical intercept is at y=3

A vertical asymptote is a vertical line that guides the graph of the function but is not part of it. It can never be crossed by the graph because it occurs at the x-value that is not in the domain of the function. A function may have more than one vertical asymptote.

`\begin{gathered} a(x)=(x^2+2x-3)/(x^2-1) \\ a(x)=\frac{(x-1)(x+3)}{(x-1)(x+1)_{}} \\ \text{hence, the vertical aymspote will be at} \\ x+1=0 \\ x=-1 \end{gathered}`

Hence,

The vertical asymptotes is at x= -1

The horizontal asymptotes will be calculated using the image below

`\begin{gathered} a(x)=(x^2+2x-3)/(x^2-1) \\ a=1,b=1,n=m=1 \\ y=(a)/(b) \\ y=(1)/(1) \\ y=1 \end{gathered}`

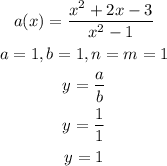
Hence,Do you have any questions about the steps to solve your question?

The horizontal asymptotes is y=1

The graph is represented below as