The slope of the tangent line to the line 2x+3y=5 can be found by differentiating 2x+3y=5.
Differentiating 2x+3y=5 with respect to x, we get
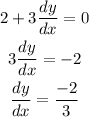
m=dy/dx is the slope of tangent line.
Hence, slope, m=-2/3.
Now, the equation of the tangent line passing through point (x1, y1)=(-2, 3) with slope m=-2/3 can be found as,
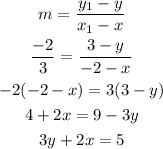
Therefore, the equation of the tangent line is 3y+2x=5.