Answer : Samuel salary falls within the standard deviation and his salary is not abnormal
The mean annual salary at the company where samuel works is $37, 000
The standard deviation is given as $4, 000
Samule's annual salary is $32, 500
Using the Z- score formula
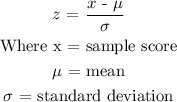
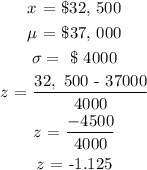
Since, the value of Z- score is -1. 125, then, the salary is 1 standard deviation below the mean.
Therefore, Samuel salary falls within the standard deviation and his salary is not abnormal