To solve this question, we proceed as follows:
Step 1: Let x be the worth of one of the type of coins Jared has, and let y be the worth of the other type of coin
Thus:
Since 3 of the coins are of a different type, we have that:
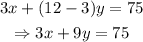
Also, since 3 of the coins are worth twice as much as the rest, we have that:
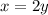
Now, substitute for x in the first equation:
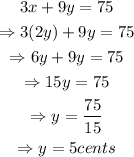
Since y = 5 cents, we have that:
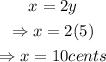
Now, since x = 10 cents (the equivalent worth of a dime), and y = 5 cents (the equivalent worth of a nickel), we have from the first equation that:
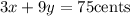
From the above equation, therefore, we can conclude that Jared has nine 10 cents coins (dimes), and three 5 cents coins (nickels)