The function we have is:
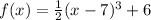
Since this is a cubic function, we start with the parent cubic function (the simplest form of the cubic function):
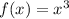
And compare it to the given function.
The first thing we can note is that there was a subtraction of 7 to the value of x:
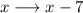
When we add a number to the x value, the graph moves to the left, and when we subtract a number to the x value, the graph moves to the right.
So the first transformation is moving to the right 7 units.
Next, we have that there was +6 added to the expression --> When you add a number to the function, the graph moves up, and when you subtract a number to the function, the graph moves down.
In this case, since we added a constant value of 6, the graph is translated 6 units up.
The second transformation is moving up 6 units.
Finally, let's analyze the effect that the 1/2 has on the function.
We can compress or stretch the graph of a function by multiplying the x by a constant (a number). If the number of between 0 and 1, there is a stretch, and if the number is greater than 1 there is compression.
In this case, the number next to the x is:
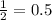
Since the number is between 0 and 1 there is a stretch of the function.
In summary:
Answer:
Translation of 7 units to the right
Translation of 6 units up
Stretch of the function of 0.5