Question

I don’t know which one it’s going to be maybe A?

Answer 1

We want to find which region has a population less than 60 animals in the diagram below

Population desity is calculated as

`\text{Population density = }\frac{\text{ number of animals }}{\text{area of region }}`

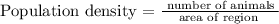
So let's get the areas of triangles A, B, C, and D we have

`\begin{gathered} \text{area of triangle =}(1)/(2)* base*\text{height} \\ A=(1)/(2)*40*35=700m^2 \\ B=(1)/(2)*50*38=950m^2 \\ C=(1)/(2)*49*42=1,029m^2 \\ D=(1)/(2)*32*51=816m^2 \end{gathered}`

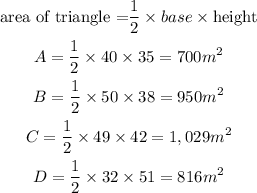
Population density for each becomes

`\begin{gathered} \text{Population density = }\frac{\text{ number of animals }}{\text{area of region }} \\ \text{For A = }\frac{\text{ 42500 }}{\text{700 }}=60.714\cong61\text{ animals } \\ \text{For B = }(60800)/(950)=64\text{ animals } \\ \text{For C = }(57300)/(1029)=55.685\cong56\text{ animals } \\ \text{For D = }(49200)/(816)=60.29\cong60\text{ animals } \end{gathered}`

Region C has a population density of 56 animals per square mile, which is less than 60.

Hence the answer is region C, option C