Question

there are 4 sets of balls numbered 1 through 12 placed in a bowl. if 4 balls are randomly chosen without replacement, find the probability that the balls have the same number. express your answer as a fraction

Answer 1

Answer:

The probability is 12/194580

Step-by-step explanation:

The balls numbered 1 through 12 are:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12

If 4 balls have the same number, then there are 12 types of this arrangement:

1, 1, 1, 1

2, 2, 2, 2

3, 3, 3, 3

and so on.

There is also 4 * 12 = 48 total number of balls.

We have a permutation:

`\begin{gathered} 48C4=(48!)/((48-4)!4!) \\ \\ =(48!)/(44!4!)=194580 \end{gathered}`

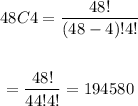
Finally, we

`(12)/(194580)`

This is the required probability.