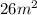The area of the composite figure can be solved by separating the figure into 3 portions, which are 2 identical rectangles with one rectangle.
The image of the composite figure will be shown below
Let us sketch out the image of the two identical rectangles
The formula for the area(A) of a rectangle is,
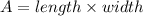
where,
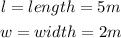
Therefore, the area(A1) of the two identical rectangles are
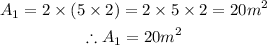
Let me sketch the second rectangle
Therefore, the area(A2) will be
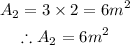
Hence, the area(A) of the composite figure is
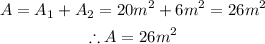
Therefore, the area is