Given:
BAC = 33 degrees
BDC = 35 degrees
Solution:
From the properties of an isosceles triangle:
The base angles of an isosceles triangle are equal. Hence from triangle BDC, we have:
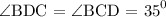
We can obtain angle DBC using the theorem that the sum of angles in a triangle is 180 degrees:
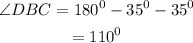
To find angle ABD, we use the theorem of congruency. i.e
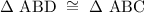
Hence,
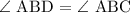
Since the angles ABD, ABC and DBC lie at a point, we have:
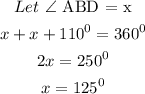
Answer : angle ABD = 125 degrees