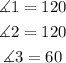Question

Find the measures of the numbered angles in the isosceles trapezoid shown below.

Answer 1

First, notice that since we have an isosceles trapezoid, the base angles will be equal, then:

`\measuredangle3=60\degree`

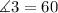
next, we have that the angles adjacent to opposite bases are supplementary, then we can write the following equation:

`\measuredangle2+\measuredangle3=180`

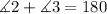
using the fact that the measure of angle 3 is 60 degrees, we can find the measure of angle 2:

`\begin{gathered} \measuredangle2+60=180 \\ \Rightarrow\measuredangle2=180-60=120 \\ \measuredangle2=120 \end{gathered}`

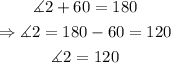
then, since angles 1 and 2 are also base angles, they are equal. Therefore, the measure of the anlges is:

`\begin{gathered} \measuredangle1=120 \\ \measuredangle2=120 \\ \measuredangle3=60 \end{gathered}`