The binomial distribution is

Therefore, in our case, the distribution is
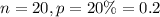
And we are interested in the probability of k=0 (0 defective bulbs) and k=1 (1 defective bulb). Thus,

Similarly,
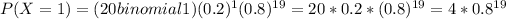
Hence,
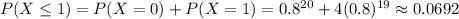
The probability of the 20 bulbs including 1 or fewer defective bulbs is 0.0692, the answer is 0.0692