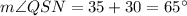Question

Heya!


`\star \underline{ \underline{ \large{ \text { {Question}}}}} :` In the given figure , PQRS is a rhombus and SRM is an equilateral triangle. If SN
`\perp` RM and
`\angle` PRS = 55° , find the size of
`\angle` QSN.

~Thanks in advance!

Answer 1

`\displaystyle\sf \angle \: QSN = {65}^( \circ)`

Explanation:

we are given a rombus and an equilateral triangle and
`\angle PRS`

said to figure out
`\angle QSN`

we know that

every angle of an equilateral triangle is 60°

so

`\displaystyle \angle SRM` should be 60°

the point where two diagonals of triangle intercept be x

recall the diagonals of a rhombus intercept each other at right angles

so
`\displaystyle \angle SXR` should be 90°

we are also given SN
`\displaystyle \perp` RM

so
`\displaystyle\angle RNS` should be 90°

notice that SXRN is a quadrilateral

so the sum of its interior angles is 360°

according to the question

`\displaystyle\sf\angle RNS + \angle SXR + \angle PRM + \angle \: QSN = 360`

substitute the value of
`\angle RNS,\angle SXR\: and \: \angle PRM`

`\displaystyle\sf {90}^( \circ) + {90}^( \circ) + {115}^( \circ) + \angle \: QSN = {360}^( \circ)`

simplify addition:

`\displaystyle\sf {295}^( \circ) + \angle \: QSN = {360}^( \circ)`

cancel 295 from both sides:

`\displaystyle\sf {295}^( \circ) - {295}^( \circ) + \angle \: QSN = {360}^( \circ) - {295}^( \circ)`

hence

`\displaystyle\sf \angle \: QSN = {65}^( \circ)`

Answer 2

`m\angle QSN=65^\circ`

Explanation:

In the given figure, PQRS is a rhombus and SRM is an equilateral triangle.

We are also given that SN⊥RM and that ∠PRS = 55°.

And we want to find the measure of ∠QSN.

Remember that since PQRS is a rhombus, the angles formed by its diagonals are right angles. Let the intersection point of the diagonals be K. Therefore:

`m\angle RKS=90^\circ`

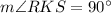
Now, RKS is also a triangle. The interior angles of all triangles must be 180. Thus:

`m\angle RKS+m\angle KSR+m\angle SRK=180`

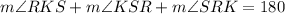
Substitute in known values:

`90+55+m\angle KSR=180`

Solve for ∠KSR:

`m\angle KSR+145=180\Rightarrow m\angle KSR=35^\circ`

Since SRM is an equilateral triangle, this means that:

`m\angle SRM=m\angle RMS=m\angle MSR=60^\circ`

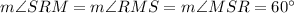
Note that RNS is also a triangle. Therefore:

`m\angle SRM+m\angle RNS+m\angle NSR=180`

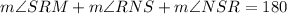
Substitute in known values:

`60+90+m\angle NSR=180`

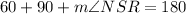
So:

`m\angle NSR+150=180\Rightarrow m\angle NSR=30^\circ`

∠QSN is the addition of the two angles:

`m\angle QSN=m\angle KSR+m\angle NSR`

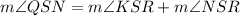
Therefore:

`m\angle QSN=35+30=65^\circ`