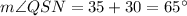Answer:
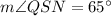
Explanation:
In the given figure, PQRS is a rhombus and SRM is an equilateral triangle.
We are also given that SN⊥RM and that ∠PRS = 55°.
And we want to find the measure of ∠QSN.
Remember that since PQRS is a rhombus, the angles formed by its diagonals are right angles. Let the intersection point of the diagonals be K. Therefore:
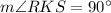
Now, RKS is also a triangle. The interior angles of all triangles must be 180. Thus:
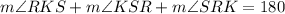
Substitute in known values:
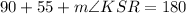
Solve for ∠KSR:
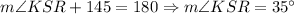
Since SRM is an equilateral triangle, this means that:
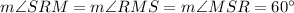
Note that RNS is also a triangle. Therefore:
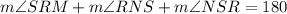
Substitute in known values:
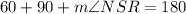
So:
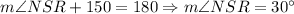
∠QSN is the addition of the two angles:
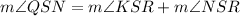
Therefore: