Question

You spin the spinner twice.678What is the probability of landing on an odd number and then landing on a 6?Simplify your answer and write it as a fraction or whole number.

Answer 1

We are asked to determine the probability of landing on an odd number and then landing on a 6.

To do that we will use the product rule of probabilities:

`P(AandB)=P(A)P(B)`

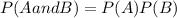
Where:

`\begin{gathered} A=\text{ landing on an odd number} \\ B=\text{ landing on a 6} \end{gathered}`

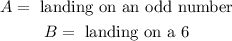
To determine the value of the probability of A we need to have into account that there is only 1 odd number (7) out of 3 possible numbers, therefore, the probability is:

`P(A)=(1)/(3)`

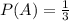
Now, to determine the value of the probability of "B" we need to have into account that there is only one number 6 out of 3 numbers therefore, we have:

`P(B)=(1)/(3)`

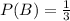
Now, we substitute the values:

`P(AandB)=((1)/(3))((1)/(3))`

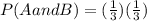
Now, we solve the operations:

`P(AandB)=(1)/(9)`

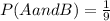
Therefore, the probability is 1/9