Let two unknow positive number is "x" and "y"
Difference of two positive number is 6 that mean:
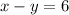
Their product is 223 less than the sum of their square:
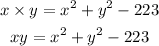
Substitute x with variable y:
So,
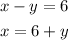
Put the value of "x" in another equation:
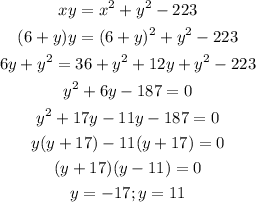
Given number is positive that mean y=11 and so value of x is:

So the number is 11 and 17.