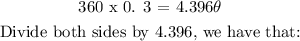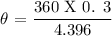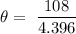SOLUTION:
Step 1:
In this question, we are given the following:
The length of an arc of a circle measures 0.3km.
The radius of the circle measures 0.7km.
What is the degree measure of the central angle of a circle associated with this arc? Use 3.14 for Π.
Round your answer to the nearest tenth.
Step 2:
The details of the solution are as follows:
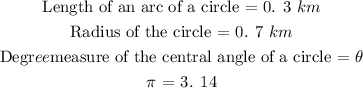

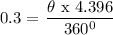
cross-multiply, we have that: