Question

Writing exponential functions (4, 112/81), (-1, 21/2)

Answer 1

The given points are (4, 112/81) and (-1, 21/2).

To find an exponential function from the given points, we have to use the forms.

`\begin{gathered} y_1=ab^(x_1) \\ y_2=ab^(x_2) \end{gathered}`

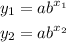
Now, we replace each point in each equation.

`\begin{gathered} (112)/(81)=ab^4 \\ (21)/(8)=ab^(-1) \end{gathered}`

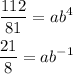
We solve this system of equations.

Let's isolate a in the second equation.

`\begin{gathered} (21)/(8)=(a)/(b) \\ (21b)/(8)=a \end{gathered}`

Then, we replace it in the first equation

`(112)/(81)=((21b)/(8))\cdot b^4`

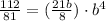
We solve for b.

`\begin{gathered} (112\cdot8)/(81\cdot21)=b\cdot b^4 \\ (896)/(1701)=b^5 \\ b=\sqrt[5]{(896)/(1701)}=\frac{2\sqrt[5]{4}}{3} \\ b\approx0.88 \end{gathered}`

Once we have the base of the exponential function, we look for the coefficient a.

`a=(21b)/(8)=(21)/(8)(\frac{2\sqrt[5]{4}}{3})=\frac{7\sqrt[5]{4}}{4}`

Therefore, the exponential function is

`y=\frac{7\sqrt[5]{4}}{4}\cdot(\frac{2\sqrt[5]{4}}{3})^x`

The image below shows the graph of this function.