Question

Gerardo is skiing on a circular ski trail that has a radius of 0.9 km. Gerardo starts at the 3-o'clock position and travels 2.6 km in the counter-clockwise direction.How many radians does Gerardo sweep out? ______radians   When Gerardo stops skiing, how many km is Gerardo to the right of the center of the ski trail?______ km   When Gerardo stops skiing, how many km is Gerardo above of the center of the ski trail? ____km

Answer 1

Circle and Angles

Gerardo is skiing on a trail that has a radius of r = 0.9 km

He starts skiing at the 3-o'clock position. This means he is initially at the right of the center of the circular trail. This position corresponds to the zero degrees (or radians) reference.

The arc length of a circle of radius r is given by:

`L=\theta r`

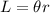
Where θ is the central angle in radians.

We know Gerardo travels L=2.6 km in the counter-clockwise direction, thus the angle is calculated by solving for θ:

`\theta=(L)/(r)\text{ }`

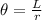
Substituting:

`\theta=(2.6)/(0.9)=2.8889rad\text{ }`

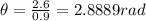
Gerardo swept out 2.8889 radians.

Now we need to calculate the rectangular coordinates of the final position where Gerardo stopped skiing. Since the angle is less than one turn of the trail, and the angle is measured counter-clockwise, we can use the formulas:

x = r cos θ

y = r sin θ

Substituting:

x = 0.9 cos 2.8889 rad

x = -0.87 km

y = 0.9 sin 2.8889 rad

y = 0.23 km

Gerardo is -0.87 km to the right of the center. In fact, he is 0.87 km to the left of the center.

Gerardo is 0.23 km above the center of the ski trail.